In Part 1 of this guide, we covered many of the basics of homomorphic encryption. In Part 2, we will discuss a practical application of homomorphic encryption to privacy-preserving signal processing.
The goal of this post is twofold:
- demonstrating that signal processing in the encrypted domain can actually be quite practical and
- providing an overview of some of the code written for Professor Gerald Penn and my paper published in Interspeech 2019 titled “Extracting Mel-Frequency and Bark-Frequency Cepstral Coefficients from Encrypted Signals.”
Real Discrete Fourier Transform
The Fourier Transform (FT) is one of the most fundamental operations in signal processing. It takes a signal from the time domain to the frequency domain. If you happen to need a primer to FT, one of the clearest explanations that I’ve found so far is in “A Student’s Guide to Waves.” If you can’t get your hands on that book, there exists a copious amount of descriptions online.
Now, for those who are already familiar with FT, you might be wondering how we can possibly convert the following formula to the encrypted domain:
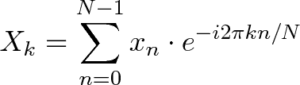
Source via Better Explained.
Well, we won’t be using the standard FT formula, since it would mean having to deal with the additional complexity of accounting for imaginary numbers within encrypted calculations. Rather, we will use the Real Discrete Fourier Transform’s (RDFT) formulae, which are very nicely described in the Real Discrete Fourier Transform publication by O.Ersoy.
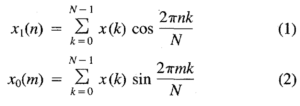
Source via IEEE Xplore.
where N is the number of samples, x(·) is the vector representing the signal, and
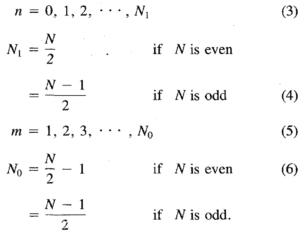
Source via IEEE Xplore.
To calculate the RDFT, we add the Discrete Cosine Transform (DCT) with the Discrete Sine Transform (DST). For simplicity, we refer to the encrypted version of values ∗ as E(∗).
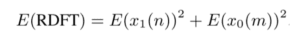
Luckily for us, cos(2πnk/N) and sin(2πmk/N) can be precomputed and do not need to be encrypted prior to multiplying the values with the encrypted signal. We prepare these values for use with the B/FV homomorphic encryption scheme from the PALISADE Lattice Cryptography Library. Note that we do need to choose a precision at which to round the values by which we will multiply our signal. We choose the number of decimal places to be retained based on a desired level of accuracy φ, then multiply the data by 10^φ (we use ^ to mean “to-the-power-of”) and round to the nearest integer.
Let’s work out the precomputations first. For the DCT, we have to calculate:

We code up the highlighted section as follows
[gist https://gist.github.com/pathaine/286c4adee2b1f78e1d2cda81a9365018 /]
And perform almost identical calculations for the DST.
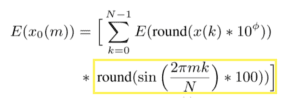
We code up the highlighted section as follows:
[gist https://gist.github.com/pathaine/1dd9e60e06b9c9311ac24de2bd18ae42 /]
I hope that these precomputations are fairly self-explanatory.
Next, we need to encrypt the signal. For our experiments, we used an audio recording of a telephone conversation from the Switchboard corpus. The kind of signal is only relevant here insofar as knowing the sample rate, which is 8kHz. In case we ever need to perform division, we create a fraction struct to store encrypted numbers. While this won’t come in handy for the RDFT calculations, it is necessary for calculating Cepstral Coefficients (which is the topic of the paper this code was originally written for).
[gist https://gist.github.com/pathaine/368d948a7625af3322dfa9a1cf1a7140 /]
We encrypt the signal as follows:
[gist https://gist.github.com/pathaine/8dc64b5bcd5544a5f3751483afc33996 /]
Now we finally have the tools necessary to calculate the RDFT:
[gist https://gist.github.com/pathaine/24842f38a0862dc07a43e6c2605d74ca /]
Performance
For a 128-bit security level, it takes 46.5235 s to calculate the RDFTs of 100 frames, given a sample rate of 16, a frame length of 25, and a shift length of 10 on an Intel Core i-7–8650U CPU @ 1.90GHz and a 16GB RAM.
These computations are, of course, parallelizable. If we were to run this code on a more powerful device and were even to adapt it to GPUs, it might become quite practical to perform encrypted FTs on the cloud.
What can we use this for?
Often, healthcare is the first sector that comes to mind when discussing sensitive data collection and processing. Audio recordings of a patient’s voice can actually contain a lot of information that’s useful for diagnosing disease (shout out to WinterLight Labs, Professor Frank Rudzicz, and Dr. Katie Fraser who have done great work on using speech processing to detect cognitive impairments like dementia).
One method for detecting pathological voices is to calculate jitter, which measures whether a gesture is sustained over a short period of time.
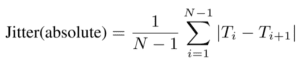
T_i ( _ used to mean subscript) are the extracted fundamental frequency (F_0) period lengths and N is the number of extracted F_0 periods
Aside from speech, images are another type of signal which can contain ample sensitive information.
The Fourier Transform is often used in image processing (e.g., for image filtering).
Interested in chatting more about encrypted signal processing? Join us for more discussion on LinkedIn, Twitter, and Youtube
Acknowledgements
This work was supported by an RBC Graduate Fellowship and the BRAIN Ontario Research Fund



